Density
Related Examples and Practice Problems
Topic Related Question Bank Categories
Density calculations: Practice using the density formula
Density comparisons: Comparing the densities to determine which will float or sink
Density and volume relationships: Changes in mass or volume affect density
Density and temperature relationships: Impact of temperature on density
Topic Summary & Highlights
and Help Videos
Core Concept
Density is the amount of mass per given volume. It is expressed as density = mass/ volume
Think of density as “how much stuff is in a given space.” Usually the space is considered a 1 cubic block, for comparisons.
Practice Tips
Master the Formula: Understand and apply Density=Mass/Volume, ensuring units are consistent.
Practice Unit Conversions: Convert between mass and volume units, like g to kg or $\text{cm}^3$ to mL.
Sink or Float: Calculate density for objects and predict if they will sink or float based on water's density.
Technique to measure volume: Use tools like water displacement for irregular volumes and lab equipment for measurements.
Solve Problems and Graph: Rearrange the formula to solve for mass or volume and graph mass vs. volume to find density.
Topic Overview Podcast
Topic Related Resources
|
LABORATORY
|
DEMONSTRATIONS
|
ACTIVITIES
|
VIRTUAL SIMULATIONS
|
Definition
Common units for density include: grams/ milliliter (g/mL) or grams/cubic centimeter (g/cm3)
Density is an intensive property meaning that it is value specific to the substance, no matter amount. If you have a huge block of copper or just a small cube -- the density of both will always be the same, since it is copper. For this reason, if you have an unknown substance you can find its density and try to match it to a list of known substances and their density to help identify it.
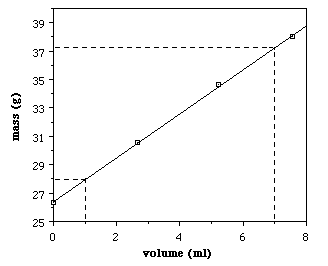
Calculating Density with a Graph:
Density on graph: y-axis is mass; x-axis is volume. Therefore the density = slope of the line.
Slope = Δy/ Δx = mass / volume (= the formula for density)
